Aufbau Rechenkompetenz
Schritt für Schritt das Rechnen automatisieren
Das Automatisieren von Grundfertigkeiten im Rechnen erfolgt Schritt für Schritt. Werden einzelne Schritte übersprungen oder übersehen, kann es zu Lücken kommen, die zu Rechenschwierigkeiten führen können.
1. Mengen- und Zahlenverständnis
Fürs Rechnen brauchen wir eine Vorstellung von Mengen und Zahlen, damit wir das Plus und Minus, das Mal und Geteilt überhaupt verstehen können. In einem ersten Schritt muss sich das Kind den Zehnerraum vorstellen können. Dafür eignen sich die Hände oder ein Steckbrett, das sie selber herstellen können.
Mengenverständnis: Lassen Sie Ihr Kind eine bestimmte Menge (z.B. 3, 6, 9, usw.) mit den Fingern zeigen (bis 5 nur eine Hand!) oder mit Legosteinen auf dem Steckbrett. Oder Sie zeigen eine Menge, die das Kind erkennen muss. Durch häufiges Wiederholen werden Gestalt und Menge auswendig gelernt.
Zahlenverständnis: Wir sehen die Zahlen innerlich in Form eines Zahlenstrahls. Das erlaubt es uns, sofort zu sagen, dass 36 eine grössere Zahl ist als 24. Zuerst kommt der Zehnerraum. Schreiben Sie auf Kärtchen je eine Zahl von 1 bis 10. Legen Sie die Kärtchen dann verdeckt auf den Tisch wie im Bild unten. Lassen Sie Ihr Kind bestimmte Zahlen suchen (aufdecken). Wo ist die 5? 3? 9? Anschliessend lassen Sie Ihr Kind die Nachbarszahlen benennen. Was kommt nach der 6? vor der 5? nach der 8? Zum Schluss fragen Sie, welche Zahl grösser bzw. kleiner ist? 6 oder 8? 9 oder 5?
Das bekannte Spiel «Elfer raus» ist eine ideale Übung für das Zahlenverständnis im 20-er Raum. Zum Üben im 100-er Raum eignet sich als Zahlenstrahl ein Meterband. Hier können Sie spielerisch vorgehen. Kleben Sie mit Klebeband eine Linie von einem Meter. Nun nennen Sie und Ihr Kind abwechselnd eine Zahl. Der eine Spieler schätzt, wo sich diese Zahl befindet und legt den Finger daneben. Dann wird gemessen. Die Abweichung wird aufgeschrieben. Wer lag weniger daneben?
2. Addition und Subtraktion im 10-er Raum
Beim Plusrechnen (Addition) sowie beim Minusrechnen (Subtraktion) handelt es sich jeweils um 45 Rechnungen (Tabelle). Diese sollten wie aus der Pistole geschossen, also in Sekundenschnelle, gelöst werden können.
Beginnen Sie Schritt für Schritt. Überprüfen Sie zuerst die Rechnungen mit +1, dann mit +2, usw. Alle Aufgaben, bei denen Ihr Kind überlegen muss, schreiben Sie auf ein Kärtchen (gleiches Verfahren wie bei Training 2). Diese müssen geübt werden. Achten Sie, dass Ihr Kind nicht mit den Fingern hinauf- und hinunterzählt. Eine Stütze sind die Hände, die auf dem Tisch liegen. Zum Beispiel 6 plus 3. Ihr Kind legt mit beiden Händen die Zahl 6. Drei Finger kommen hinzu. Das Kind zeigt die Menge 9.
Oder üben Sie die Rechnungen wie beim Training 1.
Eine gute Merkhilfe für die Plusrechnungen, welche die Zahl 10 ergeben, sind die Verliebtheitszahlen (oder auch Freundschaftszahlen). Diese nennt man so, weil sie ein Zahlenpärchen (=10) bilden.
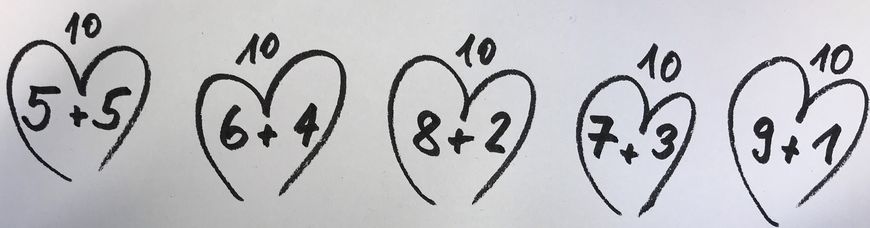
3. Addieren und Subtrahieren im 20-er Raum und 100-er Raum ohne Zehnerübergang
Sobald der Zehnerraum automatisiert ist, wird es Ihrem Kind (bald) leichtfallen, zunächst im 20-er Raum, dann im 100-er Raum (ohne Zehnerübergang!) schnell zu rechnen. Zur Stütze braucht es am Anfang vielleicht eine Veranschaulichung. 44+5=? «Wieviel gibt 4+5? Genau, 9. Wieviel gibt jetzt 44+5? Genau, 49».
4. Plus- und Minus mit Zehnerübergang
Das Einüben mit Zehnerübergang kann Kindern einfach und spielerisch erklärt werden. Dafür sollte es zuerst die Verliebtheitszahlen (oder auch Freundschaftszahlen) genau kennen, welche schon im Schritt 3 eingeübt worden sind.
Üben Sie zuerst den Zehnerübergang im 20-er Raum, erst dann im 100-er Raum.
Der Zehnerübergang am Beispiel der Addition 7 + 8 geht in Rechenschritten wie folgt:
Nach dem gleichen Prinzip verfahren Sie mit den Minusaufgaben.
Achten Sie beim Zehnerübergang im 100-er Raum auf die richtige Reihenfolge, je nach Strategie, die Ihr Kind in der Schule lernt.
5. Das kleine Einmaleins
Schrittweise können Sie das kleine Einmaleins gemäss Video Training 2 einüben. Sollte Ihr Kind mit dem Einmaleins schon vertraut sein, dieses aber noch zu wenig automatisiert haben, gehen Sie wie folgt vor:
Insgesamt handelt es sich um 100 Multiplikationen. Welche Aufgaben muss Ihr Kind noch lernen? Mithilfe der 1x1 Tabelle überprüfen Sie alle Rechnungen und notieren die Aufgaben auf Kärtchen, die Ihr Kind nicht innerhalb einer Sekunde lösen kann. Sie und Ihr Kind werden bemerken, dass schon sehr viele Aufgaben automatisiert sind. Nur schon die Einer – und Zehnerreihen können die allermeisten Kinder, womit schon 36 Rechnungen entfallen. Fahren Sie fort und Ihr Kind wird erstaunt feststellen, dass der 1x1-Berg immer kleiner wird. Das ist sehr motivierend für Ihr Kind. Mit dem einfachen Würfelspiel (zwei 10-er Würfeln) üben Sie das kleine Einmaleins.
6. Das kleine Einsdurcheins
Das gut gelernte Einmaleins bietet eine perfekte Ausgangsbasis für das Einsdurcheins (100 Aufgaben). Auch hier können Sie zuerst "durchfischen" und nur die Aufgaben auf Kärtchen schreiben, die noch nicht automatisiert sind. Los geht's.